puzzles and conundrums

complex puzzles, conundrums and exercises

Puzzles, conundrums and lateral thinking exercises help team building, motivation, and will warm up any gathering. Puzzles and conundrums like these are great brain exercises, and are good illustrations of how the mind plays tricks. See also the puzzles and tricks page, the team building games section for team building and employee motivation ideas, and try the expressions derivations quiz. Puzzles and lateral thinking exercises add interest to meetings and training sessions. Giving groups or teams a mixed set of puzzles is a great way to get people working together and using each other's strengths.

These lateral thinking exercises and complex puzzles are great for making people think, opening minds to new possibilities, and illustrating how the mind plays tricks and the importance of using the brain, instead of making assumptions.

boy girl probability puzzle

A man has two children. One of them is a boy. What's the probability that the other one is a boy?

Most people think this is the same as: A man has a child, and it's a boy. He then has another child. What is the probability that the second one is a boy too? The answer to that is 1 in 2, or 50%. It's like saying: if I toss a coin and it comes down heads, what are the odds that it will come down heads next time? But this problem is quite different. This is why:

If a man has two children, he could have had:

first a boy, then a girl - BG
first a boy, then another boy - BB
first a girl, then a boy - GB
first a girl, then another girl - GG

These are the only possible ways in which a man can have had 2 children, and they are all equally probable. The probability of each is therefore 1 in 4, or 25%. Now let's come back to the problem. We know that at least one of the children is a boy. That cuts out just one of the 4 possibilities listed above - GG - leaving 3 possibilities: BG, GB, BB (each of which, as we've seen, is equally likely). Of those 3, only one - BB - satisfies the condition that the other child is a boy as well. So the answer is 1 in 3, or 33.3% (.3 recurring to be precise).

Quite a lot of people refuse to believe this because they think that if a man has two children, he can have two boys, two girls or one of each, i.e., three possibilities, each equally likely. But they're not equally likely, because 'one of each' is not one possibility, but two. Think of all the people you know with 2 children, and you'll find that roughly a quarter of them have two boys, a quarter have two girls, and half of them have one of each. (Ack Terry Moran)

This is a classic problem arising in probability theory. The precise wording of the question, and the mathematical approach to the assumptions made affect the interpretation. I have therefore received correspondence suggesting different mathematical justification and answers for this puzzle. If you want to add your own comments feel free to contact me. More complex information about this problem is available on the web, provided by people far cleverer than me, for example: http://en.wikipedia.org/wiki/Boy_or_Girl.

A pivotal aspect of the wording is whether the probability takes account of the two children, in which case the complex statistical theory applies, or whether only the second child is accounted for, in which case the complexities disappear and it becomes a simple 50:50 question (aside of course from other marginal biological non-mathematical factors affecting tendencies, for example for female births to be very slightly more common than male births in many societies, or other influences such as diet, stress, etc., which in some cases are thought to affect male/female conception bias.)

Here is some of the feedback I've received:

From Brenda, Nov 2007: It is true that there is a 25% chance of having 2 boys if you have two children however, I don't believe the answer to this problem to be correct. The question changes based on the information provided. Both children's gender is no longer in question. The fact that one of the children is a boy leaves only 2 possibilities for the second child (a boy or a girl) therefore it is actually a 50% chance that the 2nd child will also be a boy... The question is really only asking what is the possibility of one baby being born a boy. So, the unknown one has a 50% chance of being a girl and a 50% chance of being a boy. The probability of two things happening is calculated by multiplying the % or chance that each individual event will occur. When you are calculating whether given two unknown genders the chances of have 2 boys it would look like this:

50% x 50% = 25% (so 1 out of 4 times)

If you wanted to calculate the chances of having 1 boy and girl you would first have to realize the number of combinations that there could be and calculate the % and then add them together. With 2 children the only combinations can be BG or GB the calculation would be:

(50% x 50%) + (50% x 50%) = 50%

To have two boys, knowing that one is a boy, the calculation is:

100% (because we know he is a boy) x 50% (because we don't know what the other child is yet) = 50%. Simple finite math. (Thanks Brenda, Nov 2007)

And additionally from A Harbour, Dec 2007: I just wanted to point out that the boy-girl puzzle is not quite true. The argument is mathematically sound from a point of view but makes an error. It depends on the population to which you confine yourself. If the man you seek had to tell you that he had a boy (he was not allowed to say he had a girl in the case he might have had 2 girls) then the population of the puzzle is restricted as it is detailed on the site and the odds are indeed 1 in 3. If however, the man could have told you he had a boy or a girl at his discretion then you cannot remove the girl girl option from the list of options in the same way and the odds revert to 50:50 by symmetry. To convince yourself of this get two coins and toss them. If you decide beforehand you are always going to say 'I have one tail, what are the chances of getting two tails' then you see that you have to throw away the two heads situations. If you however choose your statement after the coins come down so that you make your statement at random when you get a head and a tail and you are forced into a particular statement when you get two heads or two tails. You can then see how the odds change between 1 in 3 and 1 in 2. This is a VERY difficult problem for people to see the distinction so don't worry if it takes a while to get! The answer that is on your website is not wrong but is only one specific solution of the problem. (Thanks A Harbour, Dec 2007)

From Roger Nall, March 2008:

I'd like to add a comment to the debate about this puzzle. After many exercising hours I've come to the conclusion that 1 in 3 always holds good, and this is why: I tossed a pair of coins 100 times and got a distribution of TT=20, HH=29, TH=21, HT=30, demonstrating that 'mixed' is a double category, twice as likely to occur as HH, (equivalent to BB). I'd question Brenda's view, Nov 2007, when she asserted that 'The fact that one of the children is a boy leaves only 2 possibilities for the second child (a boy or a girl)'. In fact it leaves 1 chance of being a boy (BB) and 2 chances of being a girl (GB, BG). What does have a probability of 1 in 2 is that the label of the child will be either boy or girl, but in this case the probability of that being 'boy' is 1 in 3 and 'girl' is 2 in 3. (Thanks, Roger Nall, Mar 2008)

From Richard Macleod , May 2008:

This puzzle just goes to show how the wording of any particular problem/issue can drastically affect the result, and as such I'm afraid I disagree with both the answer provided and the alternative views offered. The question does not simply ask, "What is probability that the second child is a boy?" If it did you would merely consider that child in isolation, and to which the probability would be simply 50%. The question specifically asks, "What it the probability of the 2nd child being a boy too?" In which case you are looking at the odds of someone having two children and both of them are boys. For any two children, the possible combination of sexes and the associated probability is:

G / G : 50% x 50% = 25%
G / B : 50% x 50% = 25%
B / G : 50% x 50% = 25%
B / B : 50% x 50% = 25%

As such it makes no difference that you already know that one of the children is a boy and that the fourth possible combination of children is no longer possible, as it is the probability of such an outcome that you are being asked. So the probability of both children being of the same sex is 25%, whereas the probability of there be one of each sex 50%. No doubt others will continue to argue differently.
(Thanks, Richard Macleod, May 2008)

From Dave Scott, Jun 2009:

I too wonder if the probability depends on the wording of the question. I think we can all agree that the probability of the first child being a boy is going to be 50%. So, if I ask "A man has one child - a boy - and his wife is expecting another; what is the probability it will be a boy?" then the answer is also 50%, because the question is actually "what is the likelihood that a fertilised egg will be male or female" and in this case the number of previous children is irrelevant (unless you are suggesting the chance fertilisation is influenced by the number of previous children). Of course, we are all actually wrong, because in real life the probability is not 50-50, and depends on many factors as I think the statistics show that more males are usually conceived in times of hardship or of overpopulation!
(Thanks Dave Scott, June 2009)

From B O'Leary, October 2009:

The question does not ask for the time line of birth to be taken into account. The question treats BG and GB as meaning the same, so however they are put, BG = GB. People are bogged down in 'first child' and 'second child' when the question does not ask anyone to take this into account. They could be twins and have only a matter of seconds between them - how ridiculous is that? Or by two different mothers and born at the exact same time. I'm not sure how to put it into a mathematical equation but here goes: BG=GB/BB = 50%.

(Thanks B O'Leary, Oct 2009)

From D Silvers, Feb 2010:

The answer is none as it is stated that one of them is a boy.

closed door probability puzzle (also known as the Monty Hall problem)

This is a fabulous demonstration of the (commonly destructive) power of faith in random decision-making over simple logic and probability.

Aside from being an entertaining statistical curiosity, the puzzle demonstrates how readily many people base decisions their on instinct, and in many cases then reinforce their decision because of an entrenched personal stance in which logic and reason are utterly ignored - 'denial' being a common term for the behaviour.

The puzzle was made famous by the format of an old USA TV gameshow 'Let's Make A Deal', hosted by Monty Hall, and the conundrum is commonly referenced in various forms by scientists and writers when demonstrating widely ranging aspects of probability theory and how the mind works.

Broadly the game show conundrum was:

A contestant is shown three closed doors. Behind one door is $10,000; behind the other two is nothing (or in most versions of the story, so presumably true, a goat). The contestant is invited to choose one of the doors and keep whatever lies behind. This offers a one-in-three-chance, ie., 1/3 or 2:1, of winning. That is to say the contestant had a one in three chance of picking the right door.

When the contestant had chosen a door, Monty Hall then opened one of the other doors to reveal nothing behind it (or a goat), which left two closed doors, one with the money behind it and one with nothing (or a goat). The contestant was then asked if they wish to change their original choice (see note below), which creates the conundrum:

Have the odds changed as to which door wins and which door loses? And if so how?

What would you do? Keep your original choice, or choose the other door?

Most contestants on Monty Hall's show were apparently reluctant to change their original choice for fear that it was right, or because intuitively they felt that probability could not be altered by revealing one of the 'losing' doors. The problem is called 'counter-intuitive', because the answer seems for many to defy instinct and logic, even after it's been explained several times.

You should change your choice, and here are a couple of ways of justifying why (mathematicians and probability experts can provide plenty more complex explanation than this if you need it):

explanation 1

The door you originally chose was a one-in-three chance - ie, the likelihood of your guessing that door to be the winning door was one-in-three. The 'other' door is now a one-in-two chance, and the likelihood of your guessing the 'other' door to be the winning door is one-in-two. You are 50% more likely to correctly guess a one-in-two chance than a one-in-three chance, so pick the other door in preference to your original choice of door.

explanation 2

The door you originally chose was a one-in-three chance. The other two doors collectively represented a two-in-three chance. When one of these doors is eliminated, the two-in-three odds transfer to the other remaining door, which you should now chose in preference to your original door, which was a one-in-three chance.

Logic and the law of probability says to switch original choice and pick a different door.

If you're still in doubt, imagine there are 20 doors - one has the money, the others nothing. You pick a door, then 18 doors are opened revealing nothing, leaving your choice and the one other door. Would you change your choice now? By switching doors you'd improve your chances from one-in-twenty, to '50:50' evens, or (depending on how you look at it) arguably nineteen-in-twenty. Do you change your choice? It's staggering how many people still refuse to.

Still sceptical? How about 100 doors: Pick a door. Open 98 revealing nothing, leaving two doors, one a winner and the other a loser. Would you still prefer your original 99-to-1 shot compared to the alternative which is at worst 50:50, and arguably a massive 99% chance?

More technical explanation at http://www.io.com/~kmellis/monty.html

If you still believe (or have trouble explaining to others who believe) that it's logical to stick with your original choice, or believe that you now have a genuine 50:50 choice, here is another idea for re-thinking the puzzle:

If you choose to ignore the first stage then of course it's an equal 1 in 2 chance, but the point of the puzzle is that there was a first stage when the odds were against you. You can decide to ignore that information, but ignoring it won't change the original odds. The odds of your initially picking correctly a one-in-three or one-in-a-hundred chance do not change just because you reveal the losing options. This is the central point of the puzzle. What about starting with a million doors? If you life depended on it? Would you still say it's a 50:50 chance and risk sticking, knowing that if you stick with your original choice you would be backing a one-in-a-million shot? Try it with a pack of playing cards and and friend. Not with a million cards of course - a more manageable number - and you will see that sticking with the first choice is successful on average broadly in line with the starting odds.

Note: While the following points of interest do not alter the main principle of the puzzle in any way, I have received various correspondence as to the nature of choice offered to contestants after opening the first door in the Monty Hall Show. It has also been suggested to me that Monty Hall said in an interview that he did not recall offering contestants the chance to change their minds. If you know more about this please tell me.

This interesting insight is from R Krob (Feb 2005) - "Monty Hall did not offer the contestants a chance to change their minds about the door (only). What he did offer them was the chance to have another chance at something else, for example: Contestant chooses the third door. The first door is opened to reveal a goat. Monty would then offer he contestant a choice between their original door or what was (hidden) in a box. The box could contain another goat or a prize of less value than the main prize (for example furniture), and sometimes the 'something else' would be a known 'sure thing', for example: Contestant chooses the third door. Door one is opened to reveal a goat. The contestant would then be offered a choice between their original door or what was in the box, which would be revealed before their decision. Maybe grand prize was a truck and box prize was kitchen appliances." (Ack R Krob)

This contribution is from Yvan Auffret (October 2006) concerning a TV show in Brazil several years ago which seems to have borrowed and developed the Monty Hall puzzle format. It was described to him by a Brazilian professor of statistics Ademir José Petenate, who apparently now teaches in Campinas, Brazil and uses the show example in his classes. Yvan writes "... there is indeed a game show that is exactly what you are describing. It's one Ferrari and two goats, and if you lose you get to spend one week with the goat (followed by camera crew)..."

(Thanks also to Rupert Stubbs, Wendy Ramsay and John for suggestions and guidance.)

the prisoner's dilemma

This amazing model was based on a traditional gambling game, and brought to prominence particularly by the American political scientist Robert Axelrod. The prisoner's dilemma has been studied and discussed for decades by strategists, gamblers, philosophers, and evolutionary theorists (see note about Richard Dawkins below). It represents a fundamental aspect of thoughtful choice over unquestioning instinct, a dilemma which we see played out everywhere - from the simplest human relationship to the largest global conflict.

At its core is the question of whether to collaborate or not (called 'defect' in this model).

The question is often is a measure respectively of emotional maturity and security (enabling collaboration and trust) versus personal insecurity and fear (tending to prompt aggression, animosity, conflict and defection).

Here's how the gambling game works. At a simple level it's great for demonstrating the dangers of selfish behaviour, and the benefits of co-operation:

There are two players or teams. Each has two cards, one marked 'Defect', the other 'Co-operate'. There is a neutral banker, who pays out or collects payments depending on the two cards played. Each player or team decides on a single card to play and gives it to the banker. The banker then reveals both cards.

Here's the scoring system:

Both play the 'Co-operate' card - Banker pays each £300.
Both play the 'Defect' card - Banker collects £10
One of each card - Banker pays 'Defect' £500, but collects £100 from 'Co-operate'.

Try it. See the 'win-win' teambuilding game based on the prisoner's dilemma on the teambuilding games page.

The tendency if for each team to play Defect all the time, in hope of the big payout, and as a defence against being 'suckered' and having to pay the big fine. But where do these collective tactics lead? In the end the banker will collect all the money, albeit at £10 per round, but the banker always wins and both players always lose.

After a while, the players realise that their only hope for survival and beating the banker is to co-operate. Of course along the way, one or other players might be tempted to play 'Defect' and will collect the big payout having exploited the trust of the other side, but is this a sustainable strategy? Of course not. It reignites the tit-for-tat aggressive defence scenario when both sides play 'Defect' and both sides lose.

Try playing the game with a group of people who randomly pair up for each round (single show of cards). Again, some players will attempt a strategy of continuous 'Defect'. Their gains however will be short-lived. Pretty soon they'll get a reputation for being selfish and no-one will play them, let alone co-operate.

Professor Richard Dawkins, Fellow of New College, Oxford, provides more fascinating explanation about this model and just how fundamental it is to our existence in his book The Selfish Gene.

The model is called the prisoner's dilemma after the traditional story of two prisoners who are suspected of a crime and captured. The evidence is only sufficient to achieve a short custodial conviction of the pair, so they are separated for questioning, and each invited to betray his partner in exchange for their freedom. Not permitted to meet and discuss their decision, they each face the following prisoner's dilemma:

Both men refuse to betray each other - Each receives a 6 month sentence due to lack of evidence.
Both men betray each other - Each receives a reduced 1 year sentence because they told the truth.
One betrays while the other does not - The betrayed gets 3 years while the betrayer goes free.

average speed conundrum

A man travel by car to a destination 25 miles away. The journey was made between 7 and 9am, so the roads were congested and progress was slow. The journey took 75 minutes, which means that his average speed was 20 miles per hour. He took the same route on the return and travelling in the middle of the day made faster time: his return journey lasted just 25 minutes, meaning that his average speed fro the return journey was 60 miles per hour.

What was his average speed for the two journeys combined?

Answer.

euler puzzles

We've all seen these geometric puzzles which challenge you to trace along all of the lines, without lifting the pen from the paper and tracing each line only once. How many of these puzzles can you complete? How many of these puzzles are possible and how many are impossible? Is there a way of knowing whether a puzzle of this sort is possible without trying it? There is (see Euler's Rule). Try them first and then check the answers, as well as learn the secret.

When you know the Euler's Rule it's easy to make up your own puzzles like these, and be confident of whether they are possible or not - all you need is a pen and a flip-chart: great for coffee break diversions, team building exercises, etc.

Puzzle 1 - Easy ones first?......
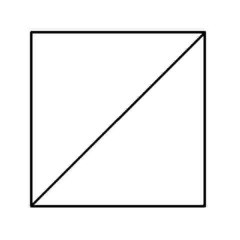
Puzzle 2 - Still easy? Can it be done?....
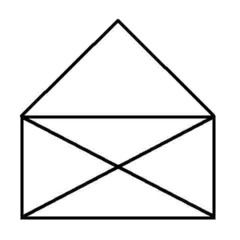
Puzzle 3 - Looks easy, but not so easy. Can it be done?
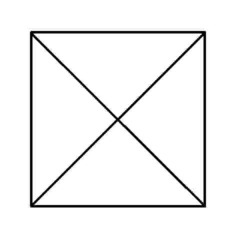
Puzzle 4 - Now this one is easy...
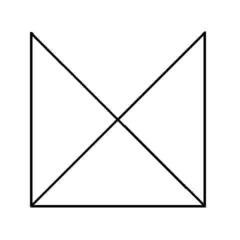
Puzzle 5 - Easy.
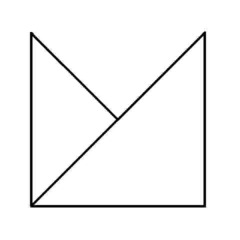
Puzzle 6 - Easy.
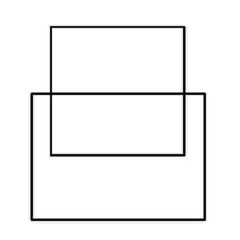
Puzzle 7 - Looks very difficult. Can it be done?
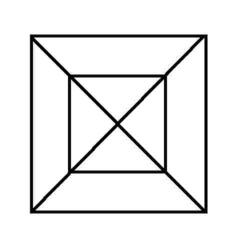
Puzzle 8 - Don't even try this one...
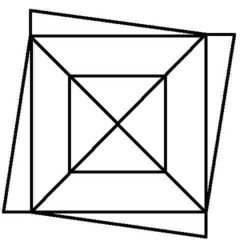
Puzzle 9 - It's got something to do with where you start...
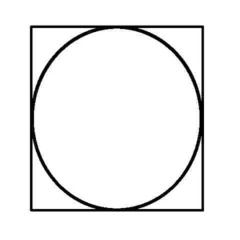
Puzzle 10 - Same applies here - where you start makes all the difference - assuming it can be done...
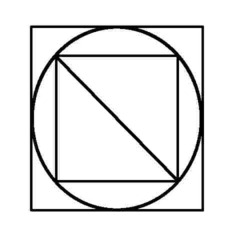
Puzzle 11 - Like I said, assuming it can be done...
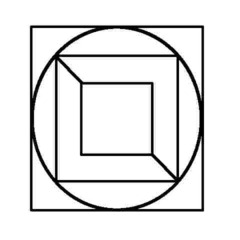
Puzzle 12 - It would be a pity to end with one that's impossible...

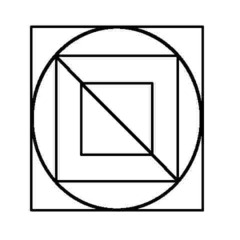
I call them euler puzzles after the man who devised the method of knowing if they are possible or not. Leonhard Euler was a brilliant 18th century mathematician who solved the puzzle of the Konigsberg bridges (now Kaliningrad, in Russia). Seven bridges connected both sides of the city and two islands in between. The townsfolk passed their time for many years trying (unsuccessfully) to find a route which would cross each bridge only once. Euler proved that is was not possible, until an eighth bridge was constructed (unfortunately little remains of the original city or its bridges since the 2nd world war). Nevertheless Euler's Rule survives, and is now used in planning routes and service territories (for postal services, meter reading, door-to-door deliveries, etc) the world over, to eliminate unnecessary travel and back-tracking. So what's the secret?

For all the answers and Euler's Rule go here.

See also the amazing Mobius Strip puzzle.

More complex puzzles and conundrums will added from time to time, so please keep visiting this page. If you have a puzzle or conundrum of your own that you'd like featured on this page (with suitable acknowledgement of course) please send it.

More quicker puzzles and tricks are on the main puzzles page.

See also the great ditloids puzzles, the cliches and words origins quiz, and the team building games section.

The use of this material is free provided copyright (see below) is acknowledged and reference or link is made to the www.businessballs.com website. This material may not be sold, or published in any form. Disclaimer: Reliance on information, material, advice, or other linked or recommended resources, received from Alan Chapman, shall be at your sole risk, and Alan Chapman assumes no responsibility for any errors, omissions, or damages arising. Users of this website are encouraged to confirm information received with other sources, and to seek local qualified advice if embarking on any actions that could carry personal or organisational liabilities. Managing people and relationships are sensitive activities; the free material and advice available via this website do not provide all necessary safeguards and checks. Please retain this notice on all copies.

average speed puzzle: 40mph? Wrong. The correct answer is 30mph. Most people's instinct is to add the 20mph and the 60mph and divide by two (20 + 60 = 80. 80 ÷ 2 = 40), which is the way most averages are calculated. But this is not the way to calculate the average of two speeds over a given distance. The correct answer can only be found by adding the distances, then adding the times, and then calculating a new average: ie., 25 miles + 25 miles = total distance of 50 miles. 75 minutes and 25 minutes = total time of 100 minutes. 100 minutes = 1.6666 (recurring) hrs. 50 miles divided by 1.6666 hrs = 30 mph.

'Euler's Rule' and the Euler puzzles answers: Impossible are 3, 7, 8 and 11. The others are all possible. Here is the secret for knowing virtually at a glance whether a puzzle like this is possible - this is 'Euler's Rule'..

The points at which lines cross or connect are called nodes. A node with an odd number of connecting lines is called an 'odd node'. An odd node is therefore a connecting or crossing point for 3, 5, 7, etc, lines. For a puzzle to be possible it must have two or no odd nodes. In other words, any puzzle with one odd node, or more than two odd nodes, is impossible. Added to which, to complete a puzzle with two odd nodes, you must begin it at one of the odd nodes and end at the other, or the puzzle cannot be completed. Now go back and try the ones you couldn't do first time, and think about what little changes could be made to the impossible puzzles to make them possible (an example is the change from puzzle 11 to puzzle 12). In Konigsberg, the bridges were effectively the lines and the river banks and islands were the nodes. The seven bridge puzzle was impossible because there were four odd nodes. The eighth bridge turned two of those odd nodes into even nodes, leaving two odd nodes and a puzzle which could then be solved.

Below is a solution to the Euler puzzle 12, if you need it, which should help you solve the others too.

Try to work it out for yourself first using the rules above (i.e., start at one odd node, and finish at the other) before resorting to the full answer.

Obviously start at point 1, which is the odd node, bottom-right, then go to 2, then 3, and so on, finishing at point 27, the other odd node, top-left.

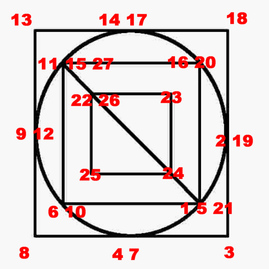
Euler's Konigsberg Bridges puzzle analysis

The river banks and islands are nodes. The bridges are effectively lines connecting these nodes. Prior to the construction of the eighth bridge (shown on the left in dotted lines, the puzzle was impossible because there were four odd nodes (count the number of bridges from each of the two river banks - 3 - and two islands - 5 and 3). When the eighth bridge was built the river bank nodes became even nodes with four bridge connections each, leaving only two odd nodes, and a solvable puzzle.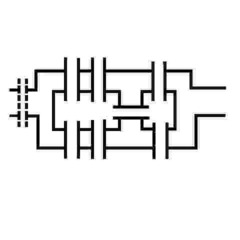

Here's a network diagram of the same thing - a topological map; the topology method of simplifying network analysis was also invented by Euler. The nodes at A and B have been changed from odd to even with the dotted line, which is the eighth bridge.

(Incidentally, the famous London Underground Map is another example of a topological map - it's not geographically accurate at all, but it is very much easier to understand than a pure geographical map.)

If you want to read more about this and other fascinating mathematical puzzles and explanations read 'Why Do Buses Come In Threes?' and the follow-up 'How Long Is A Piece Of String?' by Rob Eastaway and Jeremy Wyndham.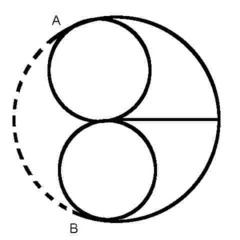

Back to to Euler puzzles.

See the Mobius Strip or Mobius Band puzzle

browse categories

business/selling
sales, marketing, strategy, business management
glossaries/terminology
glossaries, dictionaries, acronyms, lists of terms
human resources
recruitment and selection, training, job interviews
teambuilding/games
activities, games, icebreakers, quizzes, puzzles
lifestyle/environment
climate change, sleeping aids, reiki

amusement/stress relief
funny and inspirational stories, quotes, humour
personal development
personal development, self-discovery, self-help, life balance
leadership/management
delegation, motivation, change management
writing/communicating
cv templates, reference letters, resignation letters
diagrams and tools
free templates, samples, resources, tests and quizzes

related materials